
Eine seltsame Schachfigur möchte alle Felder auf einem Schachbrett besuchen und möchte dabei so wenig Weg wie möglich zurücklegen. Dabei darf sie sich aber nicht ganz frei bewegen – findest du die beste Tour?
Das TSPFN (Traveling Salesperson Problem with Forbidden Neighborhoods) ist eine Verallgemeinerung des immens wichtigen und sehr bekannten Problem des Handlungsreisenden. Bei diesem klassischen Problem geht es darum, eine kürzestmögliche Rundreise durch eine Reihe von Städten zu machen, wobei alle Distanzen bekannt sind.
Das Problem des Handlungsreisenden hat große Bedeutung im Bereich der Transportlogistik und ist ein NP-schweres Optimierungsproblem, d.h. es ist sehr schwierig (sogar für die leistungsfähigsten Computer der Welt) eine optimale Lösung in vernünftiger Zeit zu finden, insbesondere für größere Probleminstanzen mit vielen Städten.
... für Abstand $r = 1$, Abstand $r = \sqrt{2}$, Abstand $r = 2$. Das aktuelle Feld ist blau, und die verbotene Nachbarschaft ist rot markiert.
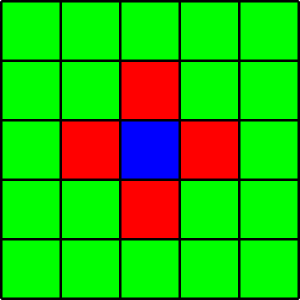
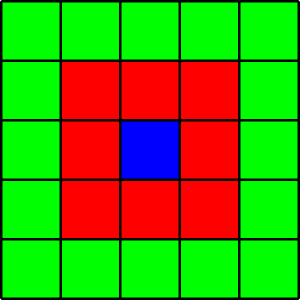
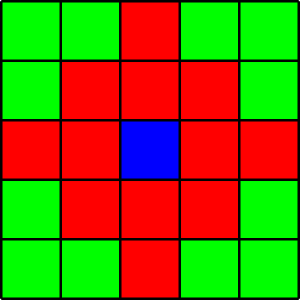
Das TSPFN baut auf dem Problem des Handlungsreisenden insofern auf, als dass bei diesem Problem eine kürzeste Rundreise $(p_0, \dots, p_{mn-1}, p_{mn})$ mit $p_0 = p_{mn}$ durch die Knoten auf einem $m\times n$-Gitter gesucht wird. Allerdings ist zusätzlich ein Parameter $r > 0$ gegeben, und es wird gefordert, dass hintereinander besuchte Knoten in dieser Rundreise einen Abstand von mindestens $r$ zueinander haben.
Es müssen also die Ungleichungen \[ \|p_i - p_{i+1}\| > r \] für alle $i\in \{0,\dots, mn-1\}$ erfüllt sein.
Das TSPFN tritt im Rahmen des Laser Beam Meltings auf. Hierbei werden Werkstücke, ähnlich wie beim 3D-Druck, in Schichten erstellt. Für jede neue Schicht muss das Werkstück an mehreren Punkten erhitzt werden.

Hier gilt es die optimale Reihenfolge zu bestimmen, in welcher die Punkte erhitzt werden, sodass die im Werkstück entstehenden Spannungen so gering wie möglich sind und zusätzlich die Produktionszeit der Werkstücke durch eine möglichst kurze Tour minimiert wird.
Einen interessanten Spezialfall des TSPFN stellt die Version dar, bei der alle Kanten bis zur Länge $r = 2$ verboten sind. In diesem Fall haben die kürzesten erlaubten Kanten die Länge $\sqrt{5}$ – Züge, die beim Schachspiel auch als Springerzug bekannt sind.

Rundreisen, bei denen nur solche Züge erlaubt sind, wurden bereits von Leonhard Euler im 18. Jahrhundert untersucht. Neu ist allerdings, dass falls eine Springertour auf einem $m\times n$-Raster existiert, diese durch ein 2007 entdecktes Schema konstruiert werden kann.

"Wer springt am besten?" wurde von den BesucherInnen zur zweitbesten Station der Langen Nacht der Forschung 2016 gewählt.